グラフ理論(Graph Theory)
グラフ理論(Graph Theory)
今
Think Complexity
グラフとは
グラフとは離散的な要素をつなぐモデルを表す抽象概念です． グラフはノード（node, 頂点（vertex））の集合と辺（edge, link）の集合で 構成されます．下図がグラフの例です．
fig.1 friendship graph
この例ではfacebookでよく見られる友達との繋がりを示しています． ノードは人を表して，異なるノード（人）が繋がっている場合は 友達であるとします．また繋がっている線を辺と呼びます． このグラフのように辺に矢印がついていないグラフを 無向グラフ（undirected graph）と呼びます．矢印がついてるグラフを 有向グラフ（directed graph）と呼びます．
上図ではBobとPaulは友達がいないため孤立点（isolated vertex）
となります．また連結（connected）していないノードがあるため，
このグラフは非連結グラフ（disconnected graph）です．
下記の図のように各ノードが他のノードに連結している場合は連結グラフと呼ばれ，さらに下図のように 各ノードから自分以外の全てのノードに連結しているグラフを完全グラフ（complete graph） と呼びます．
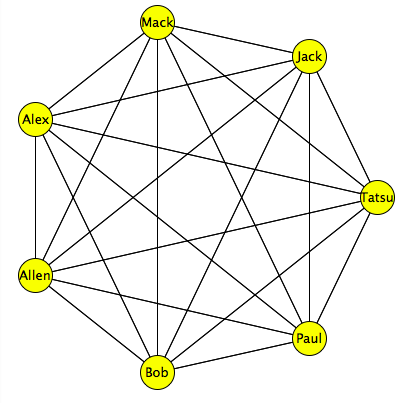
fig.2 complete graph
完全グラフでは辺の数は
n*(n - 1)/2
となります．ここでのnはノードの数です．
各ノードは自分以外のノードと連結するためn-1の辺を持ち，それが
n個あるためn倍します．しかし，重複があるので2で割ります．
そうすることで全体の辺の数を算出できます．
＊
fig.1を作成する際に異なる2つのノードとの間に辺が存在する確立をp = 0.3として
グラフを作成しました．このように確立で作成するグラフをランダムグラフ（Random
Graph）と呼びます．
グラフの簡単な紹介は終わりにして次にグラフの簡単な実装例を紹介します．
グラフの実装例
グラフの実装例は以下のようになります．
Graphは辞書を継承して作っており，main()を実行すると
Graphは以下のように出力されます．
{Vertex('v'): {Vertex('w'): Edge(Vertex('v'), Vertex('w'))},
Vertex('w'): {Vertex('v'): Edge(Vertex('v'), Vertex('w'))}}
このプログラムではkeyの値がノードを表しており，valueが連結しているノードと
その辺との辞書で表されています．g[始点ノード][終点ノード]で辺を確認する事ができます．
今回の例ではg[v][w]とするとノードvとノードwの辺であるEdge(Vertex('v'), Vertex('w')
を抽出することができます．
ランダムグラフの実装例
fig1のグラフはランダムグラフを用いて作成しました．
下記のコードではランダムグラフはグラフを継承しています．
またadd_random_edgesで任意の２つのノードを結ぶ辺を確立pで
生成します．
注意
GraphWorldはグラフを可視化するモジュールです．
こちらからインストールできます．
連結性とBFS(Breadth-first-search)
fig.1で言及した連結性は幅優先探索（BFS）
で全探索しノードの数と訪問したノードの数を比較することで
判定しました．
fig.1の連結性を判定するには
friendship_graph()に以下のコードを追加する事でできます．
print g.is_connected()
is_connected()メソッドは連結グラフでない場合はFalseを返し，連結グラフであればTrueを返します．
続いて，ノードの探索に使用したBFSについて簡単に説明します． BFSは幅を優先して探索する探索手法です． 一般的に，ノードを処理するとそのノードを訪問（visit）したといます． また，訪れたノードには印をつけ，まだ訪れていないノードの探索を行います．
BFSのアルゴリズムは以下のようになります．
- step1 任意のノードから初め，そのノードをworklist(queue)に追加する
- step2 worklistの先頭からノードを取り出し印をつける．そのノードが未探索のノードと連結していれば，連結している全てのノードをworklistの末尾に追加する
- step3 worklistが空でなければstep2に戻る
＊このアルゴリズムでの印をつける作業はclosedリストに訪問したノードを追加することで 行いました．
まとめ
以上，大まかにではありますが，グラフ，ランダムグラフ，連結性とBFSについて説明し， 実装例を紹介しました．間違っている説明などがあればご指摘ください．
